The sinusoidally driven damped pendulum as well as the Lorenz system is a system with continuous time and a three-dimensional state space. Its motion is ruled by the following set of differential equations: Here x is the angular deflection, v the angular velocity,  a damping rate, a
the driving amplitude, a damping rate, a
the driving amplitude, 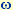 the driving frequency and the driving frequency and 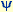 the phase of the driving torque. In an experimental realization the mass of the pendulum is mounted
at the end of a rigid rod rather than a thread. So deflections larger than 90° and even rotations of the pendulum are possible. the phase of the driving torque. In an experimental realization the mass of the pendulum is mounted
at the end of a rigid rod rather than a thread. So deflections larger than 90° and even rotations of the pendulum are possible.
Contrary to the Lorenz system here is one degree of freedom which does not depend on the others, i.e. the driving 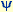 (the third equation). This is because the system is driven by an external regular sinusoidal torque whose phase
grows proportional to the time. Systems with this property are called non-autonomous. (the third equation). This is because the system is driven by an external regular sinusoidal torque whose phase
grows proportional to the time. Systems with this property are called non-autonomous. Another property that cannot be found at the Lorenz system is the periodicity of the state space. In order to
determine the pendulum's state uniquely it is sufficient to reduce both, the phase 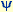 and the deflection x to the interval [- and the deflection x to the interval [- ... ... ] since it does not matter how many driving periods are passed and how many times the pendulum has
rotated to the one or the other side. ] since it does not matter how many driving periods are passed and how many times the pendulum has
rotated to the one or the other side. Depending on the driving amplitude and the driving period attractors of totally different kinds can exist. For a vanishing driving torque the neutral position (x = 0, v = 0
) is a stable fixed point (in this limit the state space is two dimensional). For small driving amplitudes the motion of the pendulum follows the driving torque with some phase
shift. The attractor now is a stable periodic orbit to which the trajectory of the pendulum converges no matter what
the initial conditions of the motion may have been. For some ranges of the driving parameters, however, the pendulum can exhibit seemingly totally irregular motions. In this chaotic regime the trajectory follows a strange attractor.
Starting from the neutral position the motion of the pendulum follows a strange attractor which is displayed
in the figure below. On the left side the pendulum and on the right side its trajectory in the state space is shown. Holding the left
mouse button pressed you can turn the state space cube to all directions . In the listbox you can choose to display not only the attractor but also some of the shortest unstable periodic orbits of
the system. With the option "manual" the scrollbars on the right side are unlocked and the driving period and frequency can be adjusted. A driven pendulum has been realized experimentally at the Physikalisches Institut der Uni Frankfurt about ten years ago and is still used for demonstrations in lectures [Heng94], [Hübinger94], [Doerner94]. At this pendulum the
predictability of low-dimensional chaotic motions has been investigated [Doerner93], [Doerner94b], [Doerner99], [Doerner99b] and the local control method has been applied [Hübinger93], [Hübinger94b], [Doerner95]
The strange attractor of the driven pendulum at the parameter values 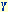 = 0.052, a = 0.586,
= 0.052, a = 0.586,  = 0.666. The direction of view is
diagonal in the state space. The red sections are Poincaré sections at = 0.666. The direction of view is
diagonal in the state space. The red sections are Poincaré sections at 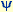 = 0 (in front on the right side) and at
x = - = 0 (in front on the right side) and at
x = -  (in front on
the left side). The vertical axis is the angular velocity. Here again (like at the Hénon attractor) the puff-pastry-like structure becomes
obvious. Also the periodicity of the structure in the directions of angular deflection and of the driving torque are visible (the back part of the structure fits to the front part in both directions). (in front on
the left side). The vertical axis is the angular velocity. Here again (like at the Hénon attractor) the puff-pastry-like structure becomes
obvious. Also the periodicity of the structure in the directions of angular deflection and of the driving torque are visible (the back part of the structure fits to the front part in both directions).      
A Poincaré section of the pendulum's attractor with the plane 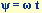 , where the time grows continously causing a movie-like
effect. The section is plotted several times in order to visualize the periodicity of the attractor in the direction of the angular deflection. , where the time grows continously causing a movie-like
effect. The section is plotted several times in order to visualize the periodicity of the attractor in the direction of the angular deflection. 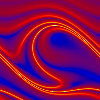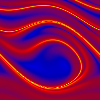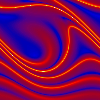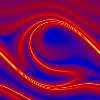     
The effective Lyapunov exponent measures the short time predictability of the motion. Here it is displayed on the Poincaré section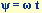 for a forecasting interval lasting one driving period. Again the time grows continuosly and again the section is plotted
several times in order to visualize the periodicity of the attractor in the direction of the angular deflection. for a forecasting interval lasting one driving period. Again the time grows continuosly and again the section is plotted
several times in order to visualize the periodicity of the attractor in the direction of the angular deflection. appendix: how to derive the dimensionless equations from the physical pendulum
A physical pendulum is characterized by its moment of inertia I (unit of measurement kg m2), its damping rate 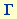 (unit of measurement kg m2s-1), the repelling moment M resulting from a deflection by 90° (unit of measurement N m = kg m2s-2
) and the sinusoidally driving torque with the amplitude A (unit of measurement N m = kg m2s-2) and the frequency (unit of measurement kg m2s-1), the repelling moment M resulting from a deflection by 90° (unit of measurement N m = kg m2s-2
) and the sinusoidally driving torque with the amplitude A (unit of measurement N m = kg m2s-2) and the frequency 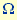 (unit of measurement s-1). Then the equation of motion reads: (unit of measurement s-1). Then the equation of motion reads: where x is the angular deflection and 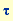 means time. This equation can be transformed into a dimensionless form
dividing it by M and substituting the time means time. This equation can be transformed into a dimensionless form
dividing it by M and substituting the time 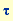 by the dimensionless time by the dimensionless time  . This last step means to measure time in units of the oscillation time of the non-driven pendulum at small deflections. This yields: Introducing new coefficients . This last step means to measure time in units of the oscillation time of the non-driven pendulum at small deflections. This yields: Introducing new coefficients 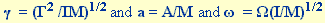 yields the equation used above. yields the equation used above. |



