|
1. Hénon-Abbildung Ebenso wie die logistische Abbildung ist das Hénon-System ein System mit einer diskreten Zeitskala n=1, 2, ... . Es besitzt einen Freiheitsgrad mehr, denn
während die log. Abbildung das eindimensionale Intervall [0..1] auf sich selbst abbildet, sind die Hénon-Gleichungen auf der reellen Ebene definiert. Außerdem besitzen nicht nur einen, sondern zwei Systemparameter, a
und b:
xn+1 = yn + 1 - axn2 |
yn+1 = bxn |
xi und yi sind die Koordinaten eines Punktes der reellen Ebene. Bei geeigneter Wahl der Systemparameter und des Startpunktes (x0 , y0)
folgen die Iterationen einer Boomerang-ähnlichen fraktalen Struktur, dem Henon-Attraktor:Per Mausrad kann man in den Attraktor hineinzoomen. Es werden jeweils 5000 Punkte innerhalb des akutellen Fensters dargestellt.
Man erkennt gut die "Blättrigkeit" dieser fraktalen Struktur. Die Werte der Systemparameter a und b lassen sich links
verstellen. Man sollte sie langsam variieren, da der Attraktor nur in einer kleinen Umgebung der Standardwerte 1,4 und 0,3 existiert.
Der Hénon-Attraktor eignet sich gut, um zwei wesentliche Charakteristika chaotischer Systeme zu veranschaulichen. Das erste ist die sensitive Abhängigkeit von den Anfangsbedingungen. Systeme, die die gleichen Systemparameter
haben, sich aber in den Anfangsbedingungen unterscheiden, und sei es noch so geringfügig, bewegen sich im Laufe der Zeit auseinander - und zwar im zeitlichen Mittel sogar exponentiell. Die zweite Eigenschaft heißt Ergodizität. Vereinfacht gesprochen verteilt sich eine große Anzahl gleicher Systeme, die zwar die gleichen Systemparameter,
aber unterschiedliche Startpunkte hatten, (ein sogenanntes "statistisches Ensemble") nach Ablauf einer hinreichend langen Zeit zu einem ansonsten beliebigen festen Zeitpunkt ebenso auf dem Attraktor wie die Folge der Iterationen
eines einzigen (fast beliebigen) Startpunktes. Anfangs zeigt das Applet eine Menge von Startpunkten, die auf der Peripherie eines kleinen Kreises liegen.
Der Kreis läßt sich per Mausklick neu positionieren. Durch Druck auf die Iterate-Taste wird die Hénon-Abbildung auf jeden dieser
Punkte einmal angewendet. Die Kreislinie wird im Laufe mehrerer Iterationen immer stärker verzerrt (sensitive Abhängigkeit von den
Anfangsbedingungen!), bis schließlich die gesamte Silhouette des Henon-Attraktors sichtbar wird. Durch Drücken der Taste
Randomize läßt sich eine völlig andere, "wolkenartige" Menge von zufällig verteilten Startwerten erzeugen. Auch hier konvergieren
die Iterationen der meisten dieser Startpunkte schließlich gegen den Hénon-Attraktor. Ein gewisser Anteil divergiert allerdings und trägt dann nicht mehr zum Bild bei. Die Ursache dieser Divergenz ist, daß das sogenannte Attraktionsbasin des Hénon-Attraktors
nicht die gesamte reelle Ebene umfaßt, sondern nur einen kleinen Bereich (ungefähr U-förmig). Schon nach wenigen Iterationen
formen die Bilder beider Mengen von Anfangsbedingungen den bekannten Attraktor, der auch von der Folge der Iterationen eines einzelnen Startpunktes gezeichnet wird (Ergodizität!).
Die Hénon-Abbildung ist dissipativ, d. h. ein Phasenraumvolumen (= ein Stückchen der x,y-Ebene) wird unter dieser
Abbildung kontrahiert, sonst könnte kein Attraktor entstehen.Man überzeugt sich davon, indem man die
Determinante der zugehörigen Jacobimatrix berechnet. Die Jakobimatrix lautet: Ihre Determinante ist somit -b. Ein Volumen wird also um den Faktor |-b| komprimiert, wenn b kleiner als 1 ist. Andere zweidimensionale dissipative Abbildungen sind z.B. die Ikeda-Abbildung, die Kaplan-Yorke-Abbildung, die Tinkerbell-Abbildung oder die Zaslavskij-Abbildung. 2. Hénons quadratische Twist-Abbildung
Von M. Hénon stammt die Untersuchung einer weiteren zweidimensionale Abbildung, deren Verhalten sich völlig von der oben beschriebenen unterscheidet, die quadratische Twist-Abbildung [Henon69]: Für den Grenzfall xn2 << yn beschreibt diese Abbildung einfach eine Drehung um den Winkel 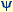 . Dieser Drehung ist eine quadratische (und somit nicht-lineare) Störung überlagert, die sich umso stärker auswirkt, je größer xn ist. Im Gegensatz zur Hénon-Abbildung ist diese Abbildung konservativ, denn ihre Jacobimatrix . Dieser Drehung ist eine quadratische (und somit nicht-lineare) Störung überlagert, die sich umso stärker auswirkt, je größer xn ist. Im Gegensatz zur Hénon-Abbildung ist diese Abbildung konservativ, denn ihre Jacobimatrix hat die Determinante 1. Somit hat diese Abbildung keine Attraktoren. Vielmehr zeigt sie das Verhalten Hamiltonscher chaotischer Systeme. Zu Beginn werden 10 Startpunkte unterschiedlicher Farbe zufällig im dargestellten Bereich der x,y-Ebene
verteilt. Jeder dieser Punkte wird dann 10000mal iteriert und die Bildpunkte werden in der gleichen Farbe gesetzt. Im Feld "psi" wird
der momentane Wert des Drehwinkels (gemessen in Radian) angezeigt und kann verändert werden. Mit der Taste "New Set" werden 10
weitere Startpunkte verteilt und wieder je 10000mal iteriert. Mit dem Mausrad kann man in die Struktur hinein-zoomen, um feine
Unterstrukturen genauer zu betrachten. Nach einem Zoom sollte man durch mehrmaliges Drücken der Taste "New Set" das Bild um
weitere Punkte anreichern.
Wie man leicht ausprobieren kann, zeigt das System für geeignete Werte von 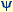 Ketten von
"Inseln", die durch "unruhigere" Bereiche von einander getrennt sind. Im Zentrum jeder solchen Insel befindet sich jeweils ein elliptischer Fixpunkt. Um diesen Fixpunkt liegt eine dichte Schicht von quasiperiodischen Orbits. Wenn
das System auf einem solchen Orbit startet, umrundet es den Fixpunkt, ohne je wieder genau seinen Ausgangspunkt zu treffen (die einfarbigen deformierten Ellipsen bestehen jeweils aus den Iterationen eines solchen Startpunktes).
Zwischen diesen "Inseln" liegen hyperbolische Fixpunkte, das sind solche, die eine stabile und eine instabile Mannigfaltigkeit
besitzen, die sich unter positivem Winkel schneiden. In der Nähe dieser Fixpunkte findet man chaotische Bereiche mit völlig irregulären Iterationen. Ketten von
"Inseln", die durch "unruhigere" Bereiche von einander getrennt sind. Im Zentrum jeder solchen Insel befindet sich jeweils ein elliptischer Fixpunkt. Um diesen Fixpunkt liegt eine dichte Schicht von quasiperiodischen Orbits. Wenn
das System auf einem solchen Orbit startet, umrundet es den Fixpunkt, ohne je wieder genau seinen Ausgangspunkt zu treffen (die einfarbigen deformierten Ellipsen bestehen jeweils aus den Iterationen eines solchen Startpunktes).
Zwischen diesen "Inseln" liegen hyperbolische Fixpunkte, das sind solche, die eine stabile und eine instabile Mannigfaltigkeit
besitzen, die sich unter positivem Winkel schneiden. In der Nähe dieser Fixpunkte findet man chaotische Bereiche mit völlig irregulären Iterationen. Literatur
Natürlich wird die Hénonabbildung ebenso wie die log. Abbildung in vielen Lehrbüchern wie z. B. [Guckenheimer83] oder [Schuster88] behandelt. Zuerst beschrieben wird sie in [Henon76]. In [Feit78] wird
numerisch die Abhängigkeit des größten Lyapunovexponenten von den Systemparametern untersucht. Hier findet man auch Darstellungen des Attraktionsbasins. Die stabilen und instabilen Mannigfaltigkeiten des Henon-Systems (und verwandter Systeme) sind Gegenstand von [Franceschini81] und [Tel82]. Um die systematische Suche nach instabilen periodischen Orbits im Hénon-Attraktor geht es in [Grassberger89]. Zur Twist-Abbildung findet man außer in [Henon69] z.B. auch in [Lichtenberg83] weitere Informationen. |